- A. Generally hyperbolic equations.
(though the definition used here is broader than
the usual math definition) Generally time-dependent problems.
|
- A. Generally elliptic or parabolic equations
(with some exceptions)
|
|
|
|
- B. Examples:
- advection eqn
- eqns of motion
- hyperbolic eqns
- many time dependent eqns (especially with propagating solutions)
- heat eqn
|
- B. Examples:
-
Poisson eqns
- LaPlace eqn
-
balance eqn
(e.g.
 2
2 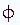 =
= (f
(f 
 )
)
-
"omega" eqn
|
|
|
|
-
C. Boundary Specifications
Consider 2nd order wave equation with 2 2nd derivatives; it still uses
just 3
boundary specifications. The idea is that the numerical soln to the
equation
at a later time t will dictate the "boundary condition" at t.
I.E. equation is solved as
initial value problem. (See figure from lecture.)
Hence, you only need keep track of the past conditions.
|
-
C. Boundary specifications
Consider (2nd order) LaPlace equation.
Here must specify all 4 boundary conditions in
order to find the solution. (Homogeneous part determined
only from boundarys.)
Hence you need a way to bring all the boundary conditions
to bear on each
interior point. Must keep track of the whole domain.
|
|
|
|
- D. Solution procedure
Usually done by retaining information in a moving "window" of time
levels.
A
direct calculation (as opposed to iteration) is generally made.
Iteration is of limited use since it is difficult to go back and revise
an earlier estimate without redoing the whole calculation.
Hence, numerical
schemes tend to be sequential
|
- D. Solution procedure
Iteration techniques can be used (since you must assess the influence
from all the boundaries, you must go over the whole grid) Direct
techniques
tend to subdivide the problem: for example, multi grid method finds
solutions on very
coarse grids then uses those to estimate the solution on finer grids.
Cyclic reduction also subdivides region
|
|
|
|
- E. Solution procedure concerns:
You want to do each (time) step in numerical sequence as accurate as
possible since you won't repeat those times. So, you look at
propagation & amplitude errors and
you also make sure that there are no compounding errors that lead to
instability
|
- E. Solution procedure concerns:
You want to make sure that your change in an estimate (when iterating)
in one
part of the domain does not excessively disturb
the solution in another part.
For direct methods, insure that errors are not magnified exeessively when
subdividing or going back to higher
resolution. In either case you want to avoid
compounding the error that may lead to instability
|
|
 2
2 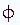 =
= )
)