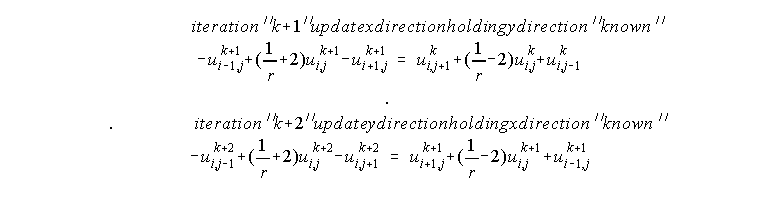• Alternating Direction Implicit: ADI

  The idea here is to keep the speed of a 1-d tridiagonal solver when solving 2-D or 3-D problems. The procedure is to split the laPlacian operator into x and y derivative parts. Then solve for values in 1 direction while holding values in the other direction.

  More specifically:

  1. Update the values in the x direction keeping the y direction values from the finite difference as "knowns" in a tridiagonal matrix inversion.
  2. Now update values in the y direction while keeping values in the x direction as "knowns".
  3. go back to step 1.

  Like SOR, it works even faster if you overcorrect. r is the overcorrection factor: 1 <= r <= 2.

  General formula:
  

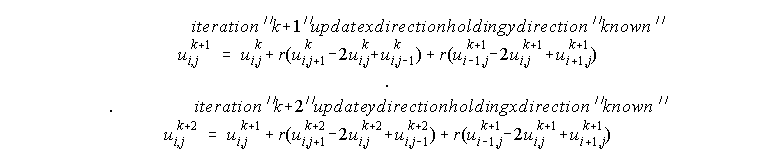
  Same formula written in tridiagonal form:
  

• Multigrid methods: (under construction)

Back to ATM 150 homepage