• I. Compilation & linking errors
  • These are generally indicated for you by cryptic messages generated at the time of compilation or linking.

  • Compilation errors are operations that FORTRAN does not allow. Examples:
    1. changing a variable defined in a parameter statement.
    2. improper do loop nesting
    3. duplicate statement names
    4. using an array as a variable or with the wrong number of subscripts. (Note: this is much harder to spot in FORTRAN 90 than it was in earlier versions, so this error is now more common.)
    5. missing statement numbers or terminators (e.g. END IF missing)

  • Linking errors are those where you ask for a subprogram that you have not made accessible. Examples are:
    • failing to include a library in your job script and
    • mispelling a subroutinename in a call statement.

• II. Excecution time errors
  • if they are recognized by the computer at all, usually show up as a number that is too large (overflow) or as an illegal number (such as requesting the inverse log of a negative number). Rather than discuss the message, it is more useful to focus on the source of the error:

  1. addresses out of array bounds
     You request or change a location in storage that is outside the space allocated to that array. Examples include:
     • incorrect passage of array dimensions to a subprogram,
     • incorrect spelling of an index or array dimension,
     • incorrect limits of a do loop index which is used in array,
     • getting the order of statements wrong (see example). The error is sometimes reported by the computer as: "operand range error"

  2. inconsistency between different parts of the program
     Examples include:
     • declaring a variable as one type but using it as another,
     • using different array dimensions in different parts of the code (may show up as an out of bounds error).

  3. a structure that does not do what is intended
     Structural errors can be wide-ranging.
     • Sometimes this is due to misunderstanding what tasks need to be performed.
     • Sometimes it is a matter of getting the order of tasks incorrect, such as placing the "time stepping" loop inside the "grid points" loop in a simulation. One can imagine many other types of structural errors....
     • other examples include: improper nesting of if-then-else statements, ...

  4. incorrectly defined or spelled variables
     Examples include
     • using 1 instead of l, 0 instead of O.
     • insufficient definitions such as PI=3.14 ( that is incorrect; instead use PI=acos(-1.) to get 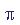to machine accuracy).
     • neglecting to pass (or redefine) a variable to a subroutine where it is used.
     • duplicate naming: avoid using variable names or subprogram names that are likely to be duplicated. (i.e. if you have a subroutine LINE, then you can't call the NCAR graphics subroutine LINE.) Note that an incorrectly spelled variable will often be treated as undefined and therefore set to the default value.

Refers to a type of error derived from the approximation in the numerical analysis scheme itself. Truncation often refers to truncating a Taylor series rep. either of a function being used or sought, or a Taylor series used in deriving a finite difference operator. This is a primary source of error in finite difference schemes.

For example, if you needed to rep exp(x) by a series, you could not use an infinite number of terms, but would have to stop ("truncate") the series after a specific number of terms. It is common practice to indicate the approx accuracy of a finite difference scheme by noting the leading term NEGLECTED in such a Taylor series. More will be said about this later.

exp(x) = 1 + x/1! +x²/2! +x³/3! + ... + _n=4 ^inf. xⁿ/n! + ...

Another type of truncation can erode accuracy and that is due to limiting the resolution of your representation. We cannot have an infinite number of grid points infinitesimally far apart.
• One must have a finite interval between grid points. The larger the interval the worse the accuracy.
• Similarly, in a Galerkin method, the more functions we have, generally the better our solution. (Galerkin methods use functions instead of grid points; e.g. Fourier Series is a Galerkin method using sines and cosines.)

The English language can sometimes be ambiguous. Sometimes the error indicated here is due to the "truncation" of the series of functions used in a spectral method. This does not make it "truncation error" as defined above it is still a matter of limited resolution. Put another way, a given grid interval, or smallest Galerkin expansion function used, determines the smallest variation you can resolve.

All computers represent non-integers with some imprecision. (Some symbolic algebra programs may work with integer parts of rational fractions to gain a bit of accuracy, but that is a software algorithm solution) Digital computers use floating point numbers of fixed word length. And this can lead to truncating the number of decimal places being kept. Generally, round off error is less when digits are rounded off (up or down depending upon the first unkept digit) than if the unkept digits are simply chopped off.

This means an error in succeeding steps depends on the error in earlier steps.

This is an error type that often occurs due to a misuse of a numeric scheme. For example, the two numerical methods: the simplest centered in time and the simplest centered in space finite differences can work in the wave equation, but will not work in the heat equation. The result always blows up. Not because the parts of the scheme are bad, but one might view it as the errors in each of the two parts interact in a pathological way.

The result of this example is typical of propagated errors in that unrealistically large, numerically infinite values are reached. The solution is useless. We refer to such a scheme as being UNSTABLE. Stable schemes either cause the errors to die out as the method continues or keeps the error within a certain bounds.

While the examples are of time dependent problems, a type of "propagated" error can also occur in diagnostic calculations when they involve either some kind of iteration or some other recursive operation (e.g. some matrix solution algorithms)

There are limits to the accuracy of your input data. Errors by the measuring devices, the representativeness of the measurement, data logging mistakes, etc. may be important to the validity of your calculation.

Also, you may be trying to represent a physical process using a mathematical formula that may not be quite right. A simple example would be using geostrophic velocities in a model instead of true velocities. I have combined these two different types of error because they are not a property of your computer or of your numerical sehcme. Nonetheless, they may be crucial to the usefulness of your answer.

With all these sources of error, you might wonder how anything can be calculated with confidence! The answer is that while numerical analysis computing opens up many problems for solution, getting that solution takes some work. Resolving and avoiding these problems is the main reason why numerical analysis is a large and highly technical field of endeavor.

Back to ATM 150 homepage