go to Examples

• Schemes:

  • 1. Trapezoidal Rule
    • Basis: sum up trapezoidal-shaped areas under the curve.
      use grid points
    • Formulation:
  
  
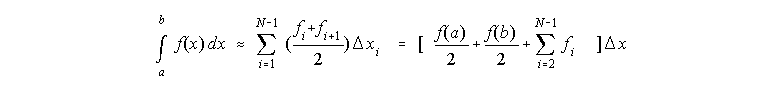
  • Ads/disads:
    1. easily understood
    2. allows variable grid point spacing
    3. fastest calculation per area used (but not fast for reaching a specified accuracy)
    4. represents integrand with straight line segments
  • 2. Romberg Integration:
    • Basis: combining two estimates gives a better estimate than either did alone. (Richardson extrapolation)
    • Formulation for estimates in ratio 2:1 for O(hⁿ) schemes:
      BE = MA + (1/{2ⁿ -1}) [MA - LA]
      BE=Better Estimate
      MA=more accurate est
      LA=less accurate est

      For example, using trapezoidal rule:

  
  
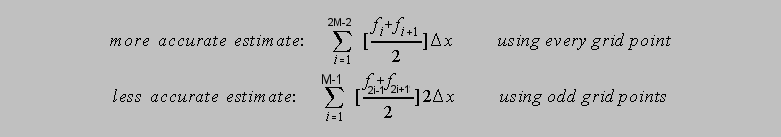
  • Ads/disads:
    1. can be applied using any integral solving scheme that satisfies the criteria
    2. requires equal grid point spacing
    3. requires a specific number of intervals (so that can subdivide)
       This can be relaxed somewhat by restricting the range used
    4. takes more calculation (but worth it!)
  • 3. Simpson's 1/3 Rule:
    • Basis:
      • Since trapezoidal rule used straight line segments, try using higher order polynomial curve segments.
        Polynomials defined by:
    
    
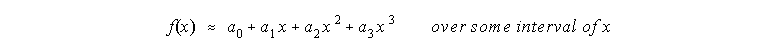
    • 2 pts determine a (straight) line; 3 pts a curve. Hence, formula will need more data points for each sub-area.
    • formulas based on Newton-Coates formulas which define polynomials based on successive grid points:
      
    
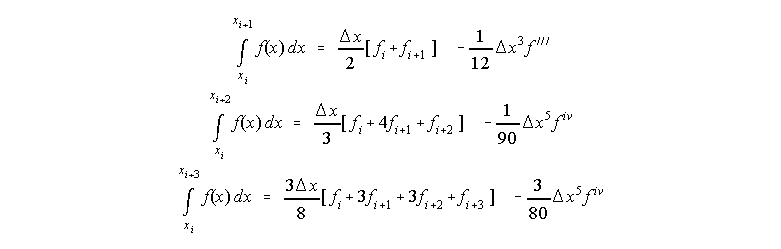
    • Formulation: see lecture notes:
    
    
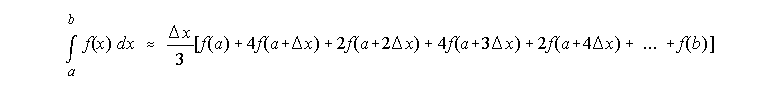
    • Ads/disads:
      1. The number of points N must be odd so that there are an even number of intervals. For example, if N=9, then there are 8 intervals. The endpoints are i =1 and 9. The coeffieient is 2 at points i=3, 5, and 7. The coefficient is 4 at points i=2, 4, 6, and 8.
      2. The grid interval must be equal.
      3. In general, the scheme will be more accurate than trapezoidal rule for a given resolution.
      4. Can apply Romberg method to Simpson's rule and get even better accuracy.
         Note: Simpson's 1/3 rule is a 4^th order scheme.
      5. As usual, more accuracy means more calculations (=computer resources) than trapezoidal rule.
      6. The cubic formula is similar, but does not seem to provide much added benefit, as mentioned above.

  • 4. Gaussian Quadrature:
    • Basis:
      • Trapezoidal, Simpson's rules represent the function with a polynomial that is 1 power less than the number of grid points used.
      • Gauss reasoned that the order of the polynomial could be increased if one added additional parameters to specify. Since he did not want to use more grid points, he allowed the locations of the grid points to be additional variables to be determined
      • here is an example using 4 unknowns: 2 weights: a & b (one for each of 2 values of f) and the 2 locations (S₁ and S₂ ) of those f values.
        The following formulas represent the integral of a single term in a polynomial in terms of the weighted polynomial at 2 points (S₁ and S₂).
    
    
    There are 4 unknowns (a, b, S₁ and S₂) and 4 equations.
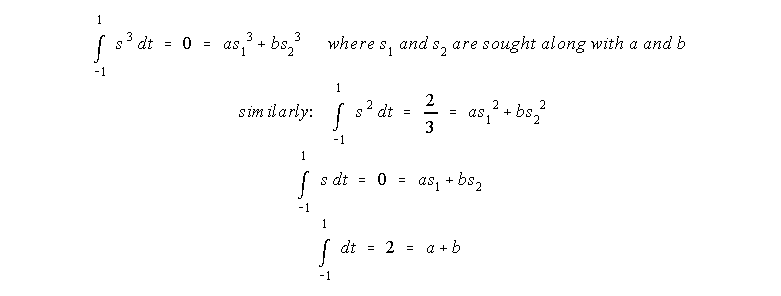
    • Formulation:

      To use Gaussian quadrature to solve a general integral, you do the following:

      1. map (or transform) the independent variable (x, say) to have the range -1. <= s <= 1. in the new coordinate t. If a <= x <= b, then a linear mapping is:

         x = {(b-a)*s + a + b}/2

      2. the mapping usually brings constants outside the integral that result from mapping dx into ds. Call those "C" such that dx = C ds. For the a to b range of x, C = (b-a)/2.
      3. When using 2 Gaussian grid points, the integral becomes simply:

         Integral from a to b of f = (b-a)/2 * [a*f(@s=-0.5773) + b*f(@s=0.5773) ]

      4. Note that the weights are trivial for 2 points: a = b = 1. When more than 2 points are used, the weights have non-trivial values.
      • For a general number of grid points:
    
    
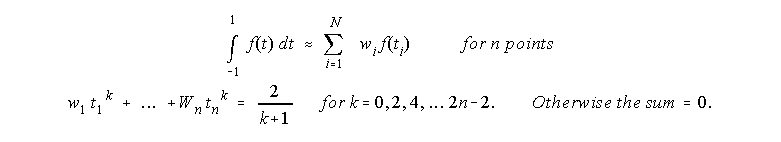
    • for 2 grid points, one obtains:
      a = w1 =1
      b = w2 =1
      s1 = - (1/3)^1/2 = - 0.5773
      s2 = (1/3)^1/2 = 0.5773
    • Ads/disads:
      1. These formulas are used by global atmospheric models that use the "spectral formulation". Such models need to make coordinate transforms in the meridional direction. The transforms are integrals and the integrand is a Legendre polynomial. Being a polynomial, using the grid defined by the Gauss formulas makes the integral exact. Clearly a powerful reason to use the scheme.
      2. While the scheme above looks easy, in practice, people use much higher order polynomials
    .

  • Examples:

    1. Trapezoidal rule and Romberg:

       Use Romberg technique to find the integral of exp(-x²) between the limits a=0.2 and b=1.5.
       The correct result (to 5 places) is 0.65882

       The largest possible grid interval is: h = (b-a)/2 = 0.65 which gives 3 (=M) grid points. The trapezoidal rule formula is quite simple:
       

       E1 = h/2 [ f(a) + f(a+h) + f(a+h) + f(b)] = 0.66211

       Subdivide this interval by using d = (b-a)/4 = 0.325 which gives 5 grid points. The trapezoidal rule formula in this case is:
       

       E2 = d/2 [ f(a) + f(a+d) + f(a+d) + f(a+2d) + f(a+2d) + f(a+3d) + f(a+3d) + f(b)]
       E2 = 0.65947

       Using EI = E2 + 1/3 ( E2 - E1 ) = 0.65859
       Clearly, this estimate is better than the ones which came before it.

       Subdivide the interval further: using D = (b-a)/8 = 0.1625, this gives 9 grid points. The trapezoidal rule is a bit lengthy to write down. When evaluated, you get the result: E3 = 0.65898 which is better than the E1, E2 or EI estimates. However, combining the E2 and E3 estimates using the Romberg formula obtains: EI2 = 0.65881. If one then combines EI and EI2 using the Romberg technique, one obtains: EF = 0.65882, the best estimate yet.

       Some books will refer to a "Romberg table" Which would have the order as follows:

       interval = h       E1                                     0.66211
       interval = d       E2     EI                             0.65947     0.65859
       interval = D     E3     EI2         EF             0.65898     0.65881     0.65882

    2. Simpson's 1/3 rule:
       
       integrate exp(-x2) between the limits a=0.2 and b=1.5.
       The correct result (to 5 places) is 0.65882

       Use a "Romberg table" to compare with Trapezoidal rule:

                         Simpson's                           Trapezoidal
       n = 5       0.65860                                           0.65947
       n = 9       0.65881       0.65882                       0.65898     0.65881

    3. Gaussian quadrature:
       • let I = intergal of sin(x)dx. from a=0 to b=/2.
         By inspection, I=1
         1. make change of independent variable to get same range: x={(b-a)s+a+b}/2
            so that dx = (( b-a)/2}* ds.
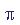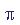         2. Making the change of variables: I = (/4) _-1¹ sin{ ( t+ 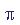)/4 } dt.
            Notice the transformed integral limits: -1 to 1.
         3. Evaluate the integrand at s = ±0.5773: I = (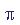/4) { 1.0*sin(0.10566 ) + 1.0*sin(0.39434 ) }
            The result is: I = 0.99847               or error R = 0.00153
       • Comparison:
         • Using 2 function evaluations with trapezoidal rule gives I=0.7854, obviously, not acceptable.
         • The mininum for Simpson's 1/3 rule is 3 evaluations, which gives I=1.0023 which is about twice the error of Gaussian quadrature (when also using 3 points).

  ---

  Back to ATM 150 homepage