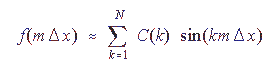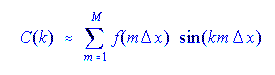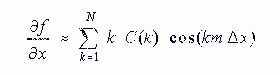A Comparison of Grid Point and Spectral Models Formulations:


 

Grid Point Model

 

Spectral Model
 
1. A field is represented by its value at discrete grid points.

.

f = f(m dx)

      Grid points:
fm         fm+1
  *             *    

  1. A field is expressed using a discrete set of coefficients of known functions.

In this example, the basis functions are sines.

 
2. Calculation is done in "real" space (at grid points)
  2. Calculation is done in "phase" space (sometimes called "spectral" space) and also in real space
 
3. Derivatives are by finite differences:

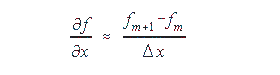
  3. Derivatives are by summing derivatives of each basis function:


 
4. Increase the resolution by choosing a smaller grid point interval: i.e. smaller dx. This means more grid points at which to make calculations.
  4. Increase the resolution by choosing a larger maximum wavenumber k. (Larger k is a smaller wavelength.)
 
5. Advantages:
  1. faster than spectral technique for equivalent resolution
  2. can "easily" handle a limited domain
  3. incorporating local processes (e.g. most physical parameterizations) is straightforward.
  5. Advantages:
  1. better approximation to derivatives, since derivative of each basis function is known.
 
6. Disadvantages:
  1. need very small dx to approximate derivatives with reasonable accuracy
  6. Disadvantages:
  1. forward and back transforms take time. The amount of calculation rises rapidly as a power of the number of grid points.
  2. can be difficult to handle non-periodic (i.e. limited region) boundary conditions
  3. local processes must be calculated while in real space (separately at each grid point)